Use the form atan(bx−c) d a tan ( b x c) d to find the variables used to find the amplitude, period, phase shift, and vertical shift a = 1 a = 1 b = 1 2 b = 1 2 c = 0 c = 0 d = 0 d = 0 Since the graph of the function tan t a n does not have a maximum or minimum value, there can be no value for the amplitude12/22/17 · Function ln(tan2x) is even Has periodicity π so I will be graphing only the interval ( − π 2, π 2) f '(x) = 1 tan2x ⋅ 2tanx ⋅ 1 cos2x f '(x) = cos2x sin2x ⋅ 2tanx ⋅ 1 cos2x f '(x) = 2tanx sin2x tanx = 0 ⇔ x = 0 x ∈ ( − π 2,0) ⇔ f '(x) < 0 ⇒ f goes down x ∈ (0, π 2) ⇔ f '(x) > 0 ⇒ f goes upI put tan 2x into an online graphic calculator, and it came up with a straight line of negative gradient going through the origin You just has the scale set wrong or something It'd be best to have it at, say, 360 degrees to 360 degrees on the x axis and 10 to 10 on the y axis?
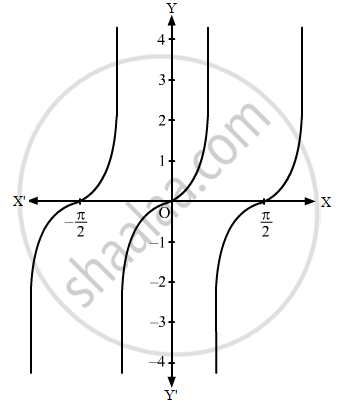
Sketch The Graphs Of The Following Functions F X Tan 2x Mathematics Shaalaa Com
Tan 1/2x graph
Tan 1/2x graph-I know homework questions are generally frowned upon here, but I've run into the following equation, which I've tried to solve and am having a genuinelyD/ (dx) (tan^2x) Derivative Calculator Symbolab This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept
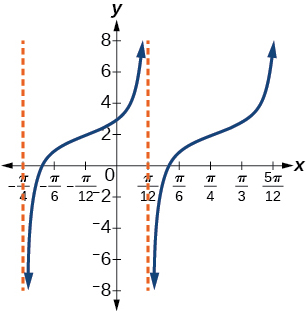


Graphs Of The Other Trigonometric Functions Algebra And Trigonometry
Y=tan 2x for the lower values of x probably does look somethingQuestion How do I graph y=3tan(2x)?//googl/JQ8NysSketch the Graph of f(x) = tan(2x)
Trigonometric graphs Higher This circle has the centre at the origin and a radius of 1 unit The point P can move around the circumference of the circle6/21/07 · y = 2tan(x) This is just a little vertical stretching Start with the graph previously described Erase whatever you labled (pi/4,1) and relable it (pi/4,2) You're almost done Relable a few more things and move on y = 2tan(2x) This is just a little horizontal compression Start with the graph previously describedSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
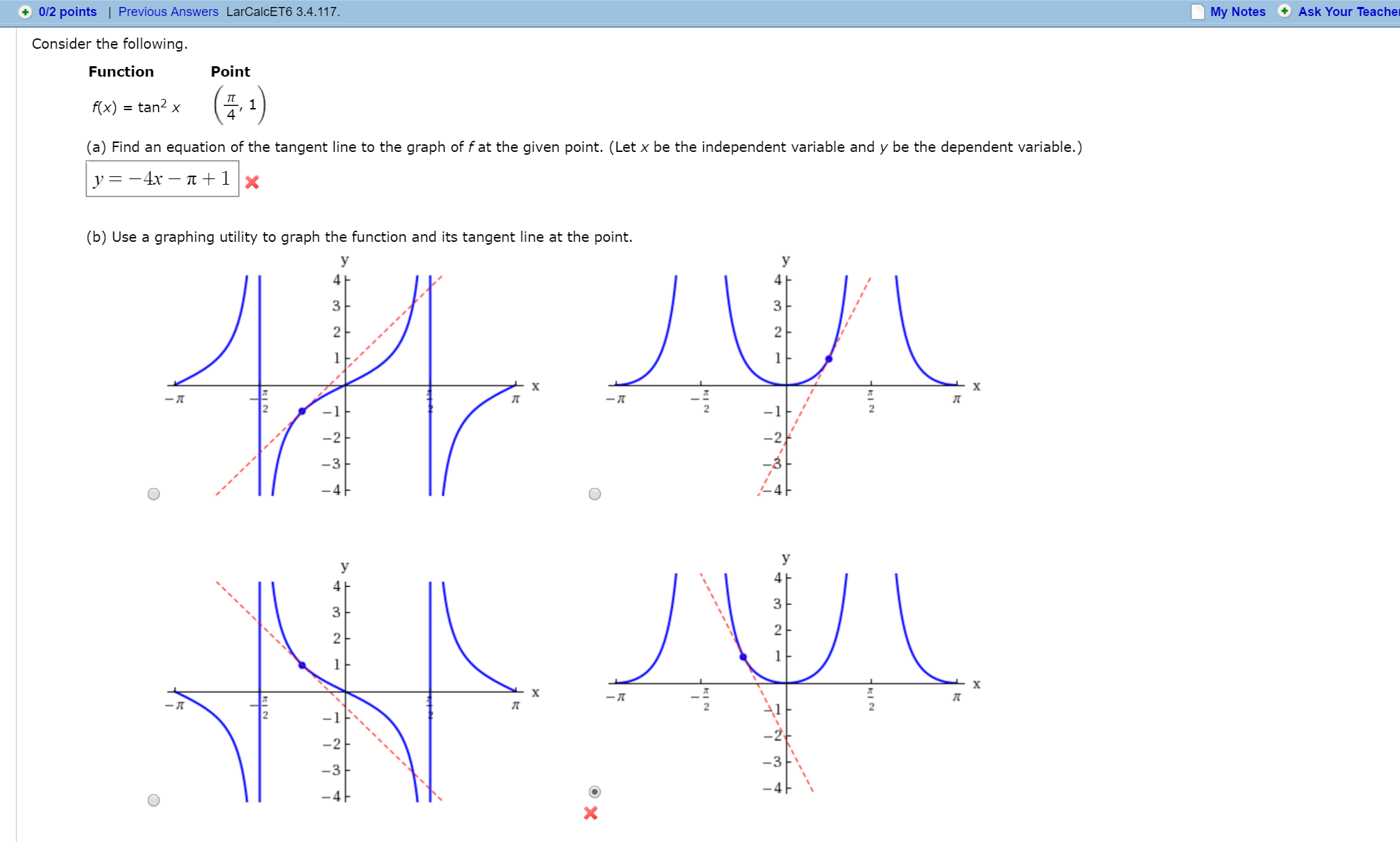
We observe that graph of y=3tan(2x) decrease between each consecutive vertical asymptotes because here amplitude a(3)Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyFind an equation of the tangent line to the graph of the function \(\ds f(x)=\tan 2x\) at the point \(\left(\frac{\pi}{8},1\right)\text{}\) Solution The slope of the tangent line at any point on the graph of \(f\) is given by


Find The Period Of Tan 2x Class 10 Maths Cbse


Graphing Tangent Functions
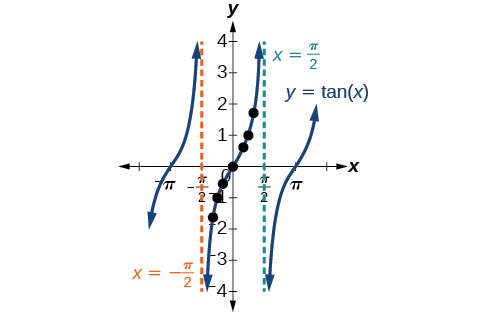
4/15/18 · The Graph of y = tan x Sketch y = tan x Solution As we saw above, `tan x=(sin x)/(cos x)` This means the function will have a discontinuity where cos x = 0 That is, when x takes any of the values `x = , (5π)/2, (3π)/2, π/2,` ` π/2,` ` (3π)/2,` ` (5π)/2, ` It is very important to keep these values in mind when sketching this graphIdentity tan (2x) Multiple Angle Identities Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to Sum12/21/ · Where the graph of the tangent function decreases, the graph of the cotangent function increases Where the graph of the tangent function increases, the graph of the cotangent function decreases The cotangent graph has vertical asymptotes at each value of \(x\) where \(\tan x=0\);
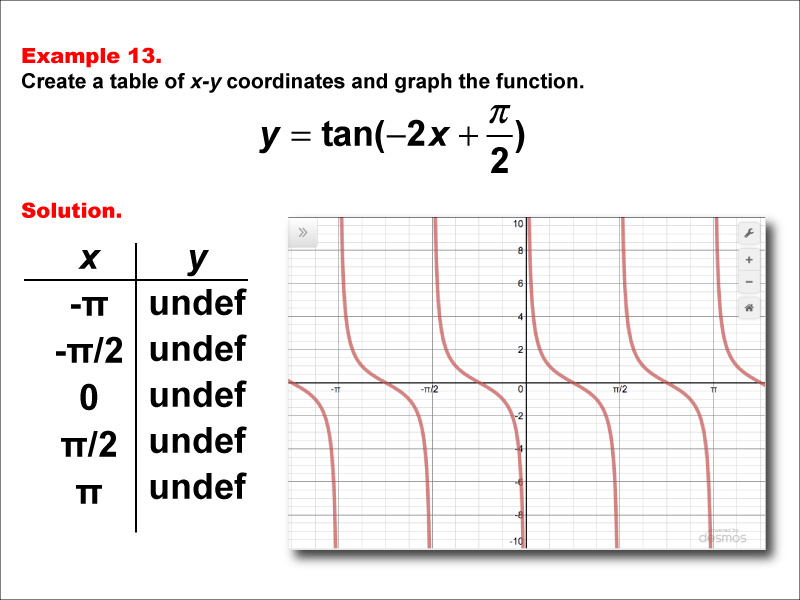


Math Example Tangent Functions In Tabular And Graph Form Example 13 Media4math


Sketch The Graph Of F X Tan 2x Youtube
(a) Sketch, for O < x < 2m, the graph of y = sin x (2) (b) Write down the exact coordinates of the points where the graph meets the coordinate axes (c) Solve, for 0 < x 21v, the equation sin x 065, (3) (5) giving your answers in radians to 2 decimal places 19/ 102/27/14 · Will, tan(x) has singularities (function goes to infinity) at pi/2 / n*piSo when you plot over the range from2*pi to 2*pi the data points just before and right after such a singularity will also be connected (by the default line), unless you tell MATLAB to ploint data points only (markers, essentially) For example,6//18 · (ii) (a) Sketch the graph with equation yx=−4 a where a is a positive constant State the coordinates of each point where the graph cuts or meets the coordinate axes (2) Given that 49xa−=a where a is a positive constant, (b) find the possible values of xx−63a giving your answers, in terms of a, in their simplest form (5)


Solved Consider The Following Function F X Tan 2 X Poi Chegg Com


4 Graphs Of Tan Cot Sec And Csc
Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example \(Tan 2x =\frac{2tan x}{1tan^{2}x} \)Graphing One Period of a Stretched or Compressed Tangent Function We can use what we know about the properties of the tangent function to quickly sketch a graph of any stretched and/or compressed tangent function of the form latexf(x)=A\tan(Bx)\\/latex We focus on a single period of the function including the origin, because the periodic property enables us to extend the graphWe show these in the graph below with dashed lines


Graphs Of Other Trigonometric Functions Ppt Video Online Download



Solved Graph The Function Over One Period Interval Y Ta Chegg Com
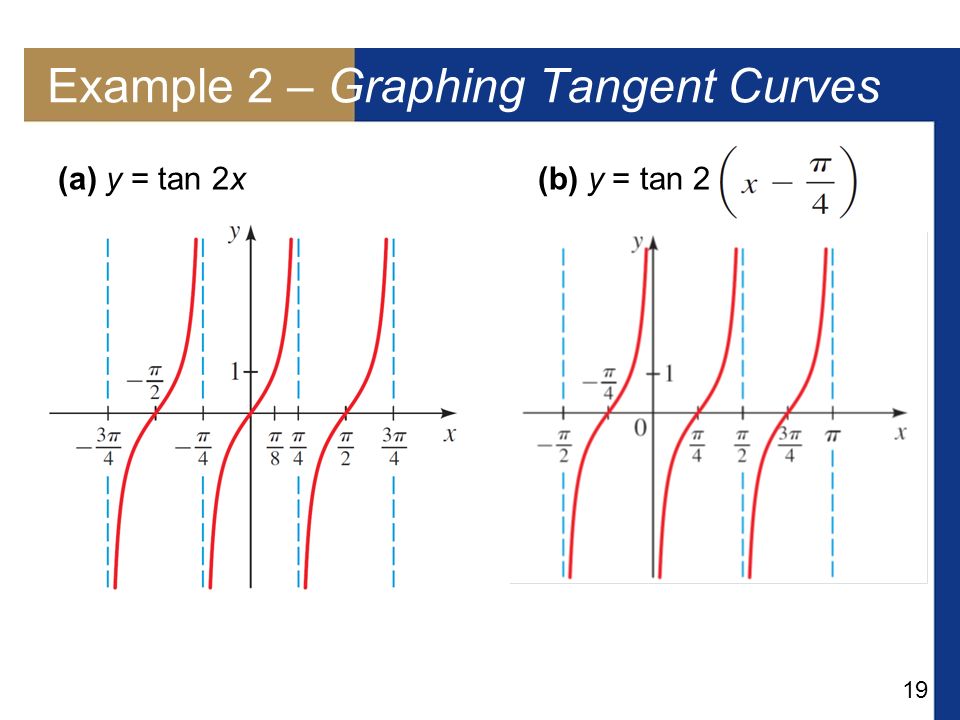
The tangent function has a parent graph just like any other function Using the graph of this function, you can make the same type of transformation that applies to the parent graph of any function The easiest way to remember how to graph the tangent function is to remember that some interesting things happen toSolution With your calculator set in radian mode, graph the three functions in the ZTrig window (press ZOOM 7) The graphs are shown below All three graphs have the same period (\(2\pi\)) and midline (\(y=0\)), but the graph of \(f\) has amplitude 2, and the graph of \(g\) has amplitude 05Multiply 2 2 by 2 2 x = π 4 x = π 4 x = π 4 x = π 4 x = π 4 x = π 4 The basic period for y = tan ( 2 x) y = tan ( 2 x) will occur at ( − π 4, π 4) ( π 4, π 4), where − π 4 π 4 and π 4 π 4 are vertical asymptotes ( − π 4, π 4) ( π 4, π 4) The absolute value is the distance between a



Ex 6 3 Q10 F X Tan 2x Sketch The Graphs Of The Following Functions
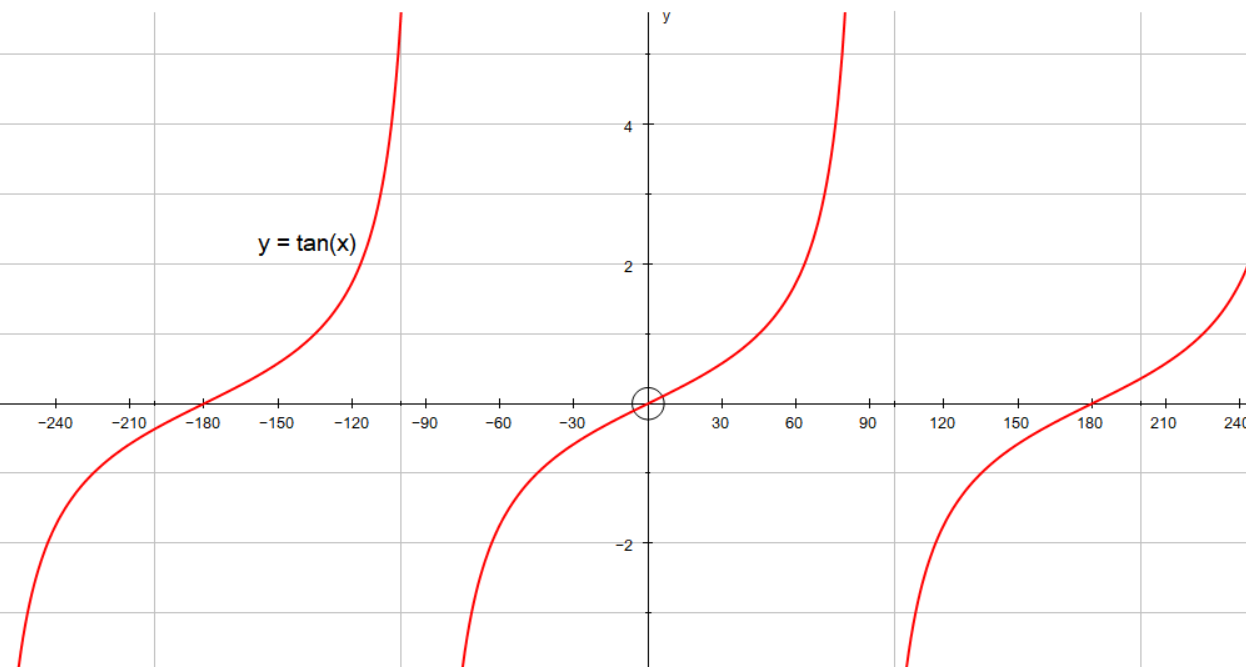


How Do You Graph And List The Amplitude Period Phase Shift For Y Tan X 60 Socratic
= 2cos2(x)−1 = 1−2sin2(x) tan(2x) = 2tan(x) 1−tan2(x) Formules du demiangle cos 2(x) = 1cos(2x) 2 sin (x) = 1−cos(2x) 2 tan(x) = sin(2x) 1cos(2x) = 1−cos(2x) sin(2x) En posant t = tan x 2 pour x 6≡π 2π, on a cos(x) = 1−t2 1t 2, sin(x) = 2t 1t et tan(x) = 2t 1−t · Somme, différence et produit cos(p)cos(q) = 2cos pPurplemath In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right trianglesThere are loads of trigonometric identities, but the following are the ones you're most likely to see and use6/28/14 · tan = O/A = 1/1 = 1 I personally don't know why they don't like irrational numbers in the denominator of fractions, but they don't So they usually convert that fraction (in both sin and cos) by multiplying by √2/√2 sin = O/H = 1/√2 = 1/√2 * √2/√2 = (1*√2) / (√2*√2) = √2/2 cos = √2/2



Sketch The Graphs Of The Following Functions F X Tan 2x Mathematics Shaalaa Com


Solution Show Me The Graph Of Y Tan2x Step By Step And How To Solve Keypoints
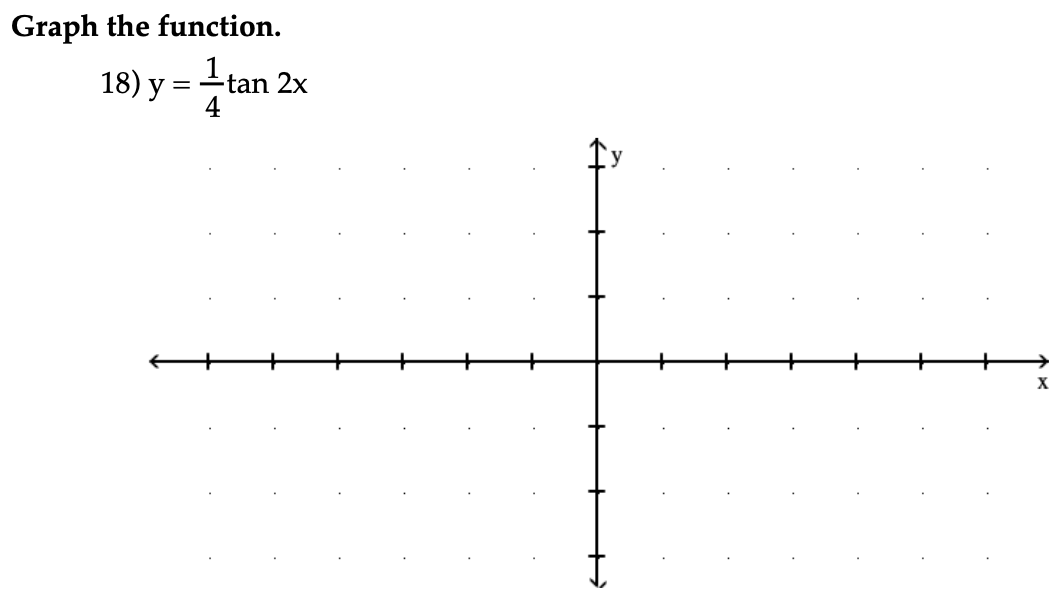
5/22/18 · Please Subscribe here, thank you!!!Graph a Transformation of the Tangent Function (Period and Horizontal Shift) y = A tan (B(x D)) C • Tangent has no amplitude • π/B is the period • C is the vertical translation • D is the horizontal translation Example y = 3 tan (2x π/2) 1 Find the period of the function 2 Find the horizontal shift 3 Graph the functionTrigonometric Equations Calculator online with solution and steps Detailed step by step solutions to your Trigonometric Equations problems online with our math solver and calculator Solved exercises of Trigonometric Equations
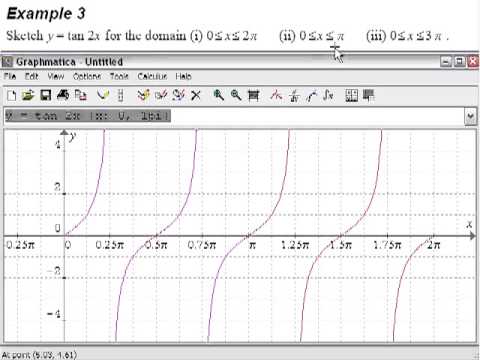


6 Trigonometry Graph Example 3 Sketch Y Tan 2x Youtube



Graphing Tangent Read Trigonometry Ck 12 Foundation
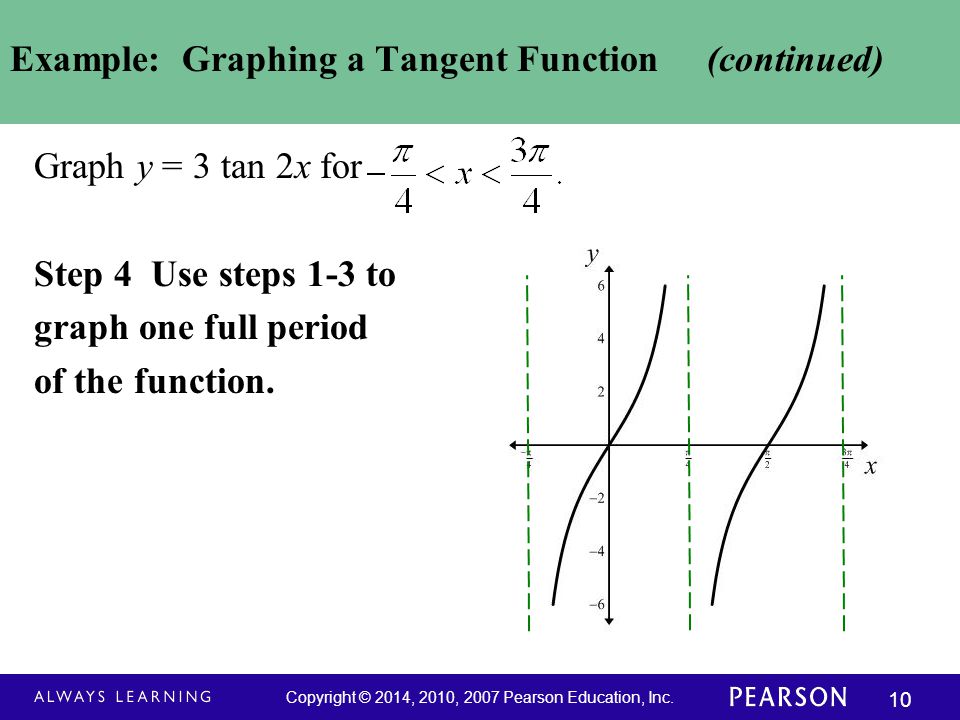
To graph a tangent function, we first determine the period (the distance/time for a complete oscillation), the phase s Learn how to graph a tangent functionGraph y=3tan(2x) Equation of tan function y=Atan(BxC), period=π/B, phase shift=C/B, A is a multiplier that stretches the curve verticallyCan you please go step by step, I have a test coming up Answer by lwsshak3() (Show Source) You can put this solution on YOUR website!
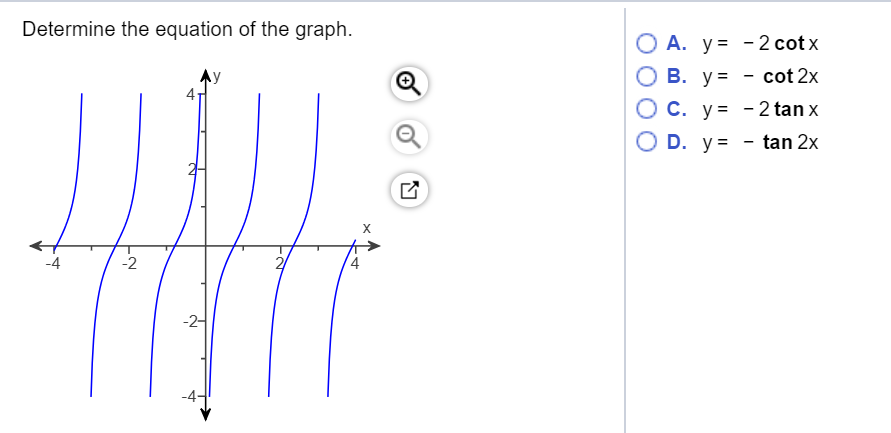


Solved Determine The Equation Of The Graph 2 Cotx Ov U Chegg Com


Solution Graph One Complete Cycle Of Y 1 Tan 2x Pi 4
The interactive function graphs are computed in the browser and displayed within a canvas element (HTML5) For each function to be graphed, the calculator creates a JavaScript function, which is then evaluated in small steps in order to draw the graph While graphing, singularities (e g poles) are detected and treated speciallyThe interactive function graphs are computed in the browser and displayed within a canvas element (HTML5) For each function to be graphed, the calculator creates a JavaScript function, which is then evaluated in small steps in order to draw the graph While graphing, singularities (e g poles) are detected and treated specially5/21/12 · How do you determine a linear function from a table and graph?


Content Graphing The Trigonometric Functions
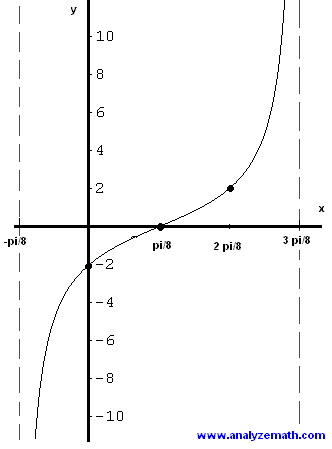


Graphing Tangent Functions
Free Online Integral Calculator allows you to solve definite and indefinite integration problems Answers, graphs, alternate forms Powered by WolframAlphaRelated » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes10/27/10 · In this graph, the cosine curve is shown in gray, and the secant curve in blue y = cos x (in gray) and y = sec x (in blue) One more step we need the square of the secant graph values that is, we are going to graph y = sec 2 x To do that, we just take each yvalue of the secant curve and square it So for example the point (105, 2) on the y = sec x curve becomes (105, 4) on the



Tan Graphs Circular Functions


Answered Graph The Function 18 Y Tan 2x Bartleby
Graph of ln(x) ln(x) function graph Natural logarithm graph y = f (x) = ln(x) ln(x) graph properties ln(x) is defined for positive values of x ln(x) is not defined for real non positive values of xThe six trigonometric functions can be defined as coordinate values of points on the Euclidean plane that are related to the unit circle, which is the circle of radius one centered at the origin O of this coordinate system While rightangled triangle definitions allows for the definition of the trigonometric functions for angles between 0 and radian (90°), the unit circle definitions allowSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more


Solution Y 2 Tan 2x Graph Two Periods Of The Given Tangent Function



The Tangent Function Functions Siyavula
Describe how to sketch the graph ofy = tan(2x) 3 using the parent function Start by graphing the tangent function Compress the graph horizontally by making the period onehalf pi Reflect the graph over the xaxis Shift the graph up 3 unitsIn fact ,there are infinite solutions, you can realise it easily,here x=tanx ,so let y=x(1) and y=tanx(2) ,for (1) ,you'll get a straight line and for (2) ,it's tan curve,the intersection of both graph will give you solution points,as (1) and (2Related Questions Browse All Math Latest answer posted August 22, 12 at AM `tan^2 x = 3 tan x`



Graphing Tangent Read Trigonometry Ck 12 Foundation



Find The Roots Of The Function Mathematics Stack Exchange
Arctan definition The arctangent of x is defined as the inverse tangent function of x when x is real (x ∈ℝ) When the tangent of y is equal to x tan y = x Then the arctangent of x is equal to the inverse tangent function of x, which is equal to y arctan x= tan1 x = y Example


Solution Graph Y 1 2 Tan 2x Pi 2 And The Period And Phase Shift


Graphs Of Trigonometric Functions Symmetry With Respect To


Derivative Of Tan X


What Is The Graph Of Mod Of Tan X Quora


What Is The Graph Of Y 1 2 Tan X Socratic



The Sine Cosine And Tangent Functions
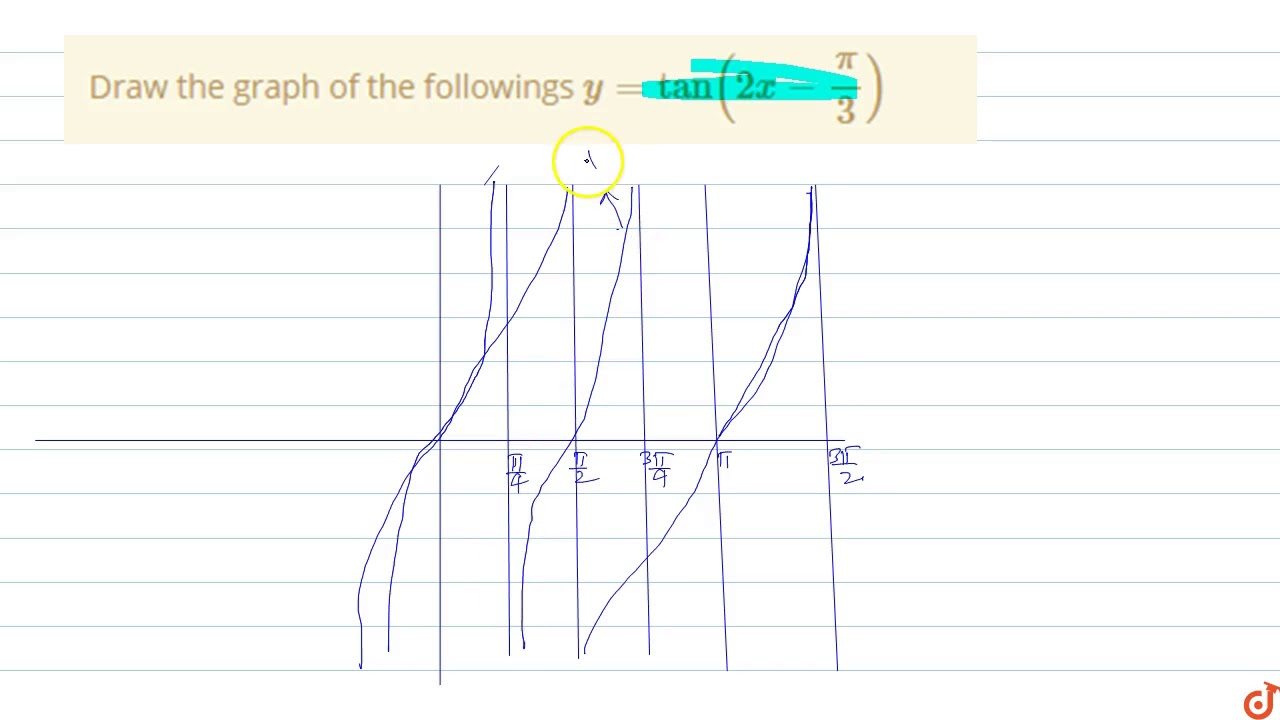


Draw The Graph Of The Followings Y Tan 2x Pi 3 Youtube



Tangent Graph


Howto How To Find Vertical Asymptotes Of Tan2x Cute766
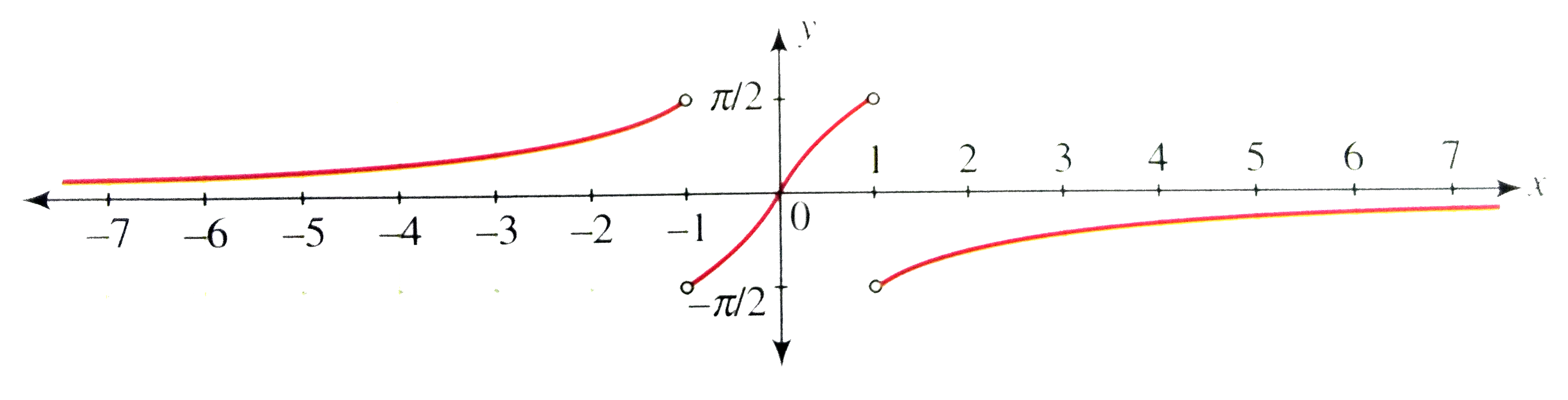


Draw The Graph Of Y Tan 1 2x 1 X 2



What Function Represented By Graph Answer Choices Y Tan 2 Theta Y Tan 1 2 Theta Y Tan Theta Y Tan Brainly Com



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



Tangent Graph


4 Graphs Of Tan Cot Sec And Csc
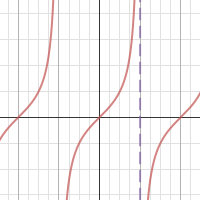


Tan Graph


Long Question 3 User S Blog



Solved Sketch The Graph Of The Following Functions Y Tan 2x Y Self Study 365
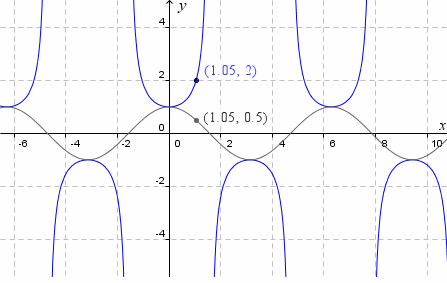


Explore The Slope Of The Tan Curve
.png)


Sketch The Graph Of The Following Function On The Same Scale 10 Y Tan 2x Y Maths Meritnation Com
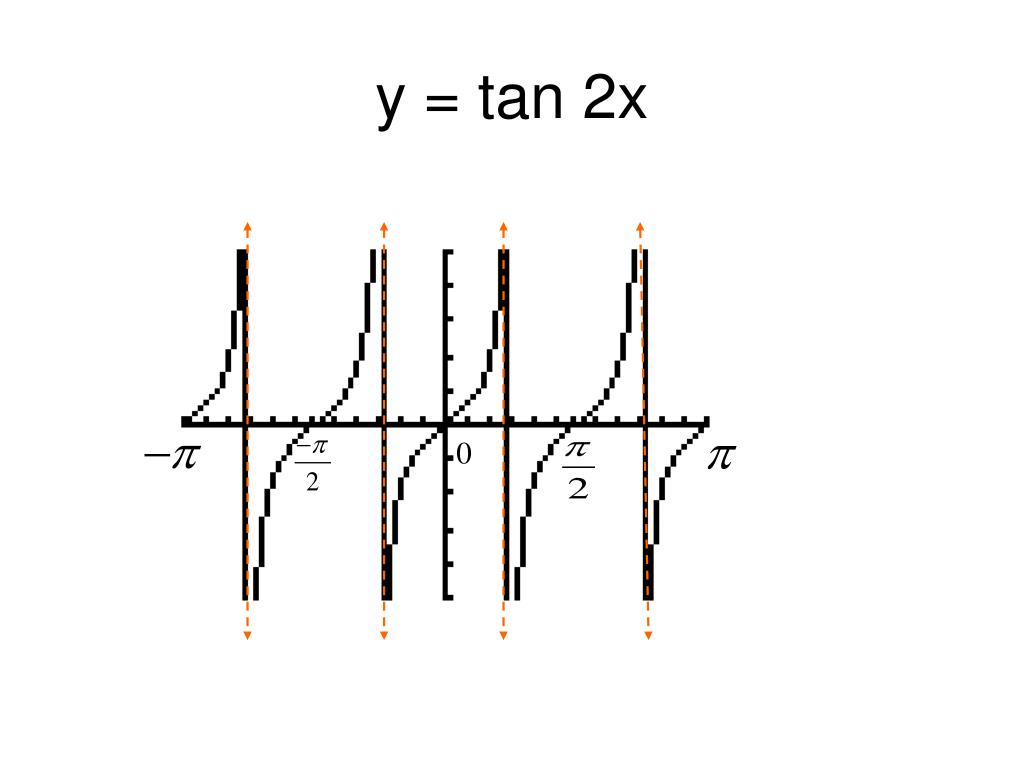


Ppt Graphing Tangent Powerpoint Presentation Free Download Id
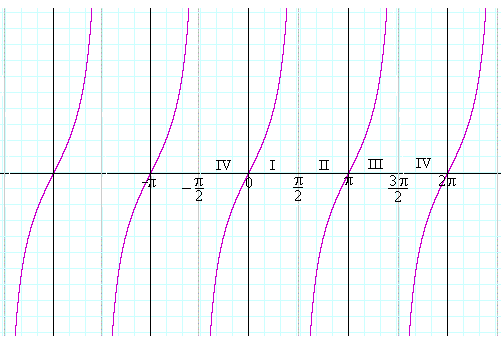


Graphs Of Trigonometric Functions



How To Graph Tan Ex Y Tan2x Study Com
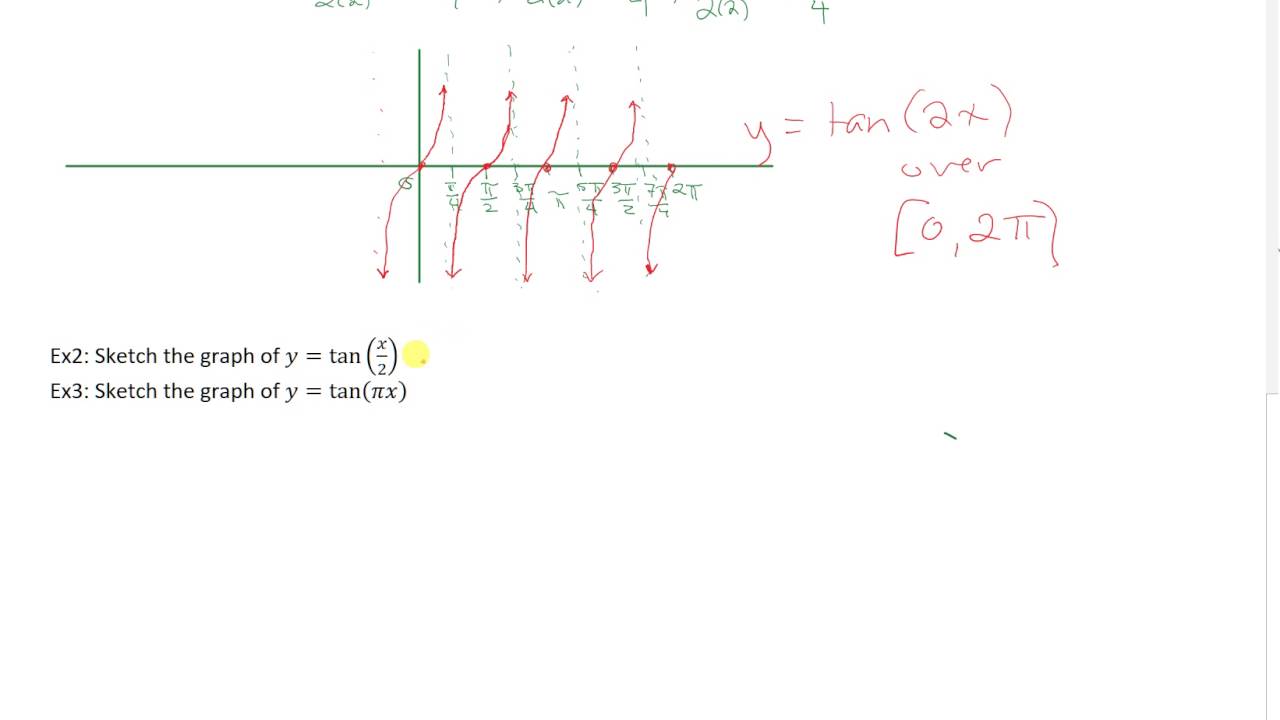


Sketching Y Tan 2x And Y Tan X 2 Youtube



Tangent Graphs Worked Solutions Examples Videos



Sketch The Graph Of The Tangent Curve Y Tan 2x In The Interval From 0 To 2pi Brainly Com


Trigonometric Graphs And Transformations Tan And Cot
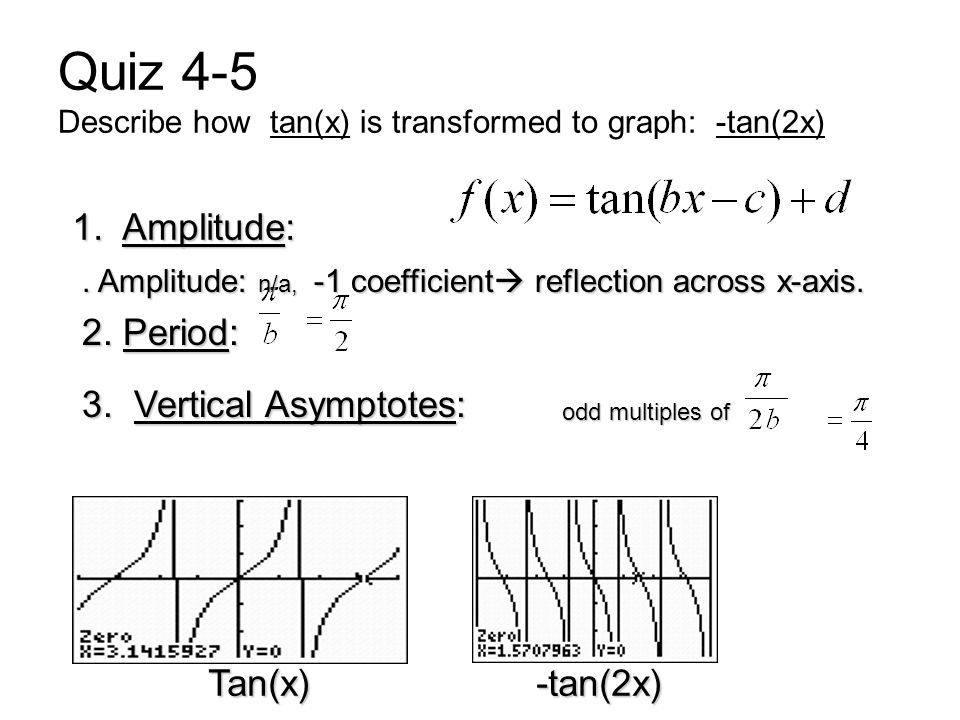


Quiz 4 5 Describe How Tan X Is Transformed To Graph Tan 2x Ppt Download


Math Scene Trigonometry Functions Graphs Of Trig Functions Lesson 3
.png)


Sketch The Graphs Of The Following Functions 4 Y Tan 2x Math Meritnation Com
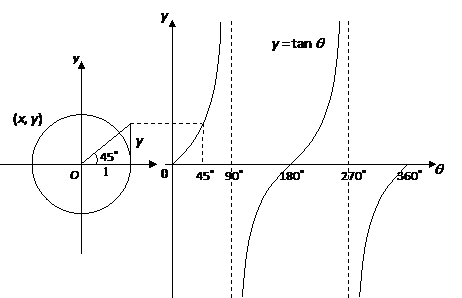


Tangent Graphs Worked Solutions Examples Videos
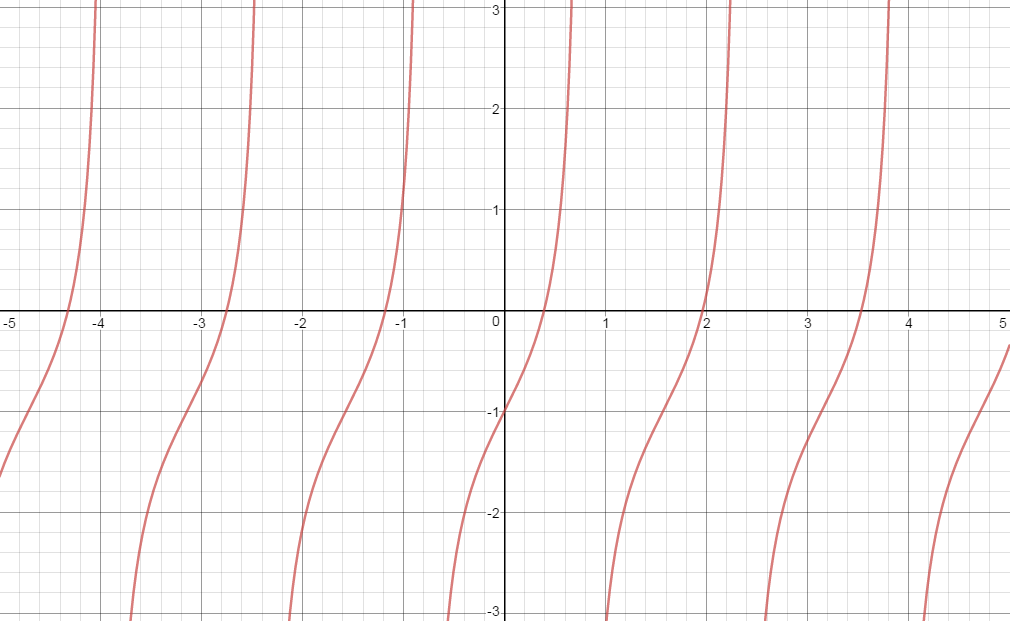


How Do You Graph Y 1 Tan2x Socratic


Graph Tangent And Cotangent
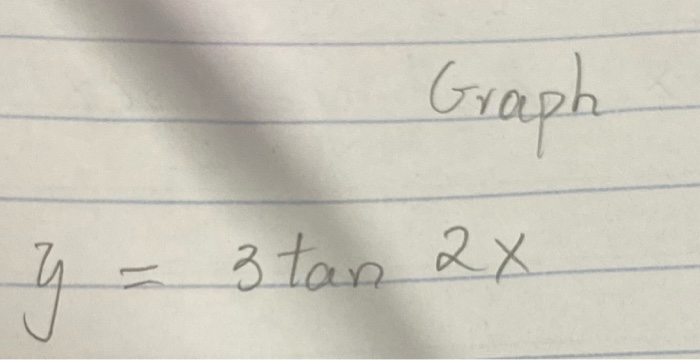


Solved Graph Y 3 Tan 2x Chegg Com



Graphs Of The Other Trigonometric Functions Algebra And Trigonometry


Graph Tangent And Cotangent



Tangent And Cotangent Graphs Ck 12 Foundation
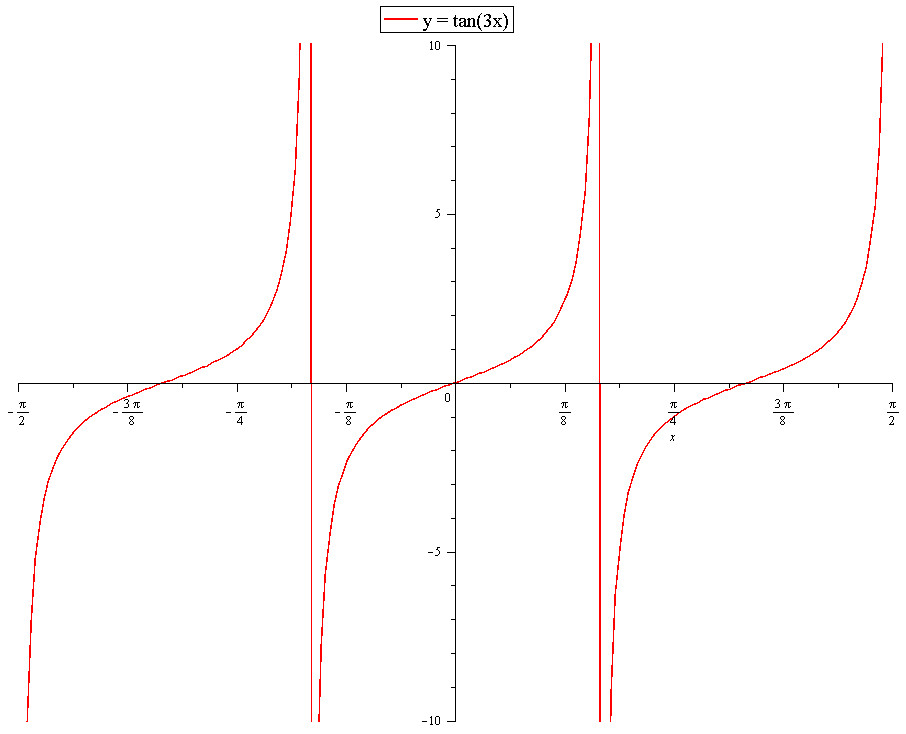


How Do You Graph Y Tan3x Socratic



Sketch The Graph 1 Y Cos 2 X 2 Y Tan2x 3 Y Sin2x Maths Trigonometric Functions Meritnation Com


Howto How To Find Vertical Asymptotes Of Tan2x
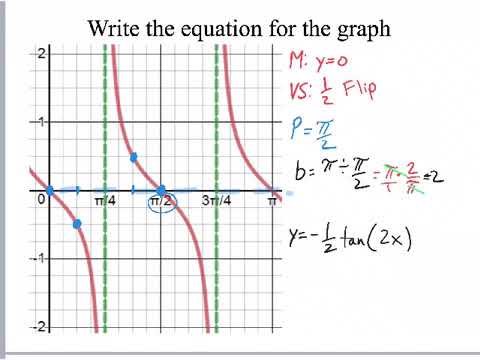


Writing Equations For Tangent Graphs Youtube


Graphing Tangent Functions


Review Cocalc
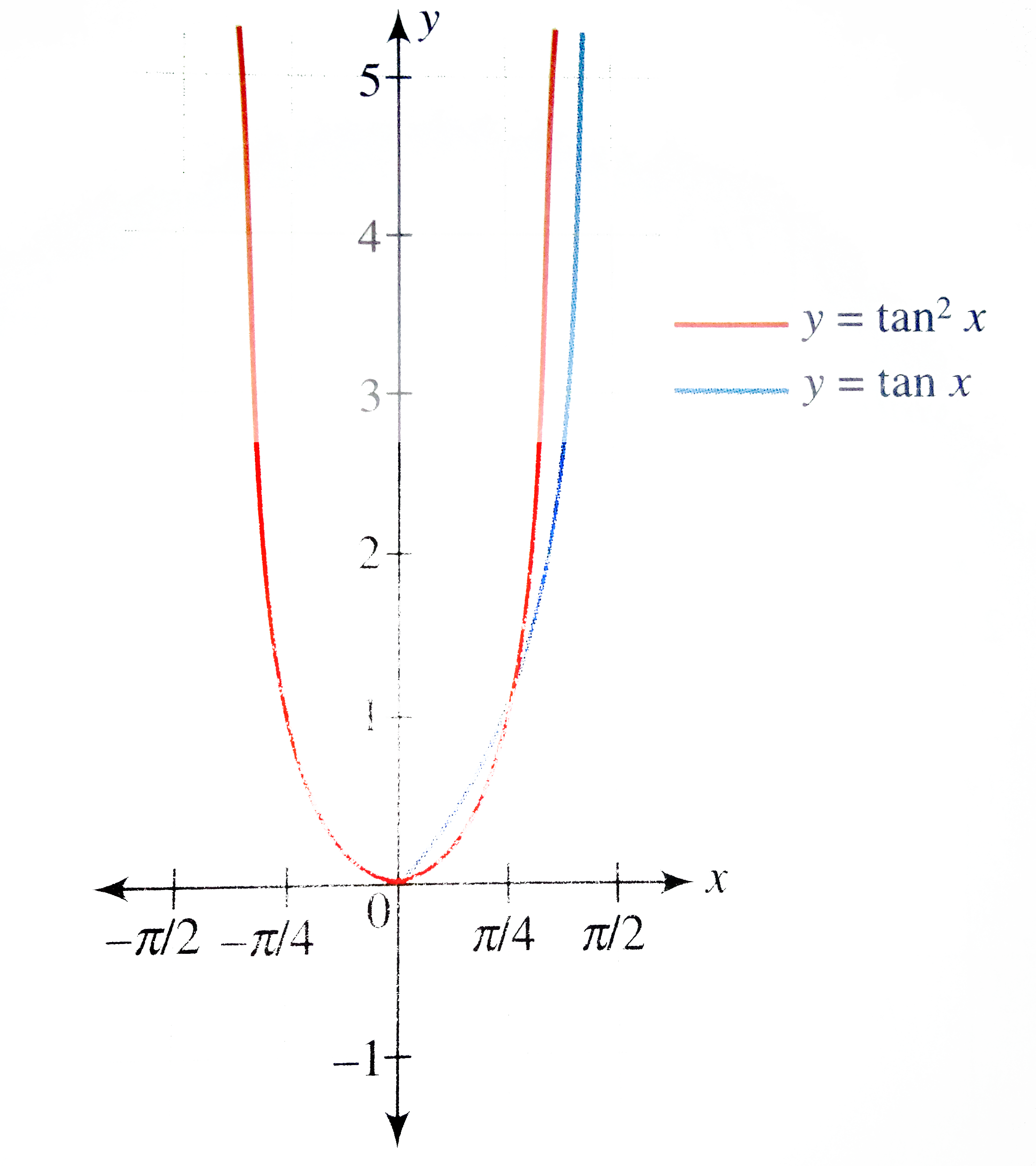


Draw The Graph Of Y Tan 2 X



Solved Graph The Function Show At Least Two Periods On T Chegg Com



Trig Transformations Of Graphs


Solution Determine The Period Of Y Tan 2x



The Tangent Function Functions Siyavula
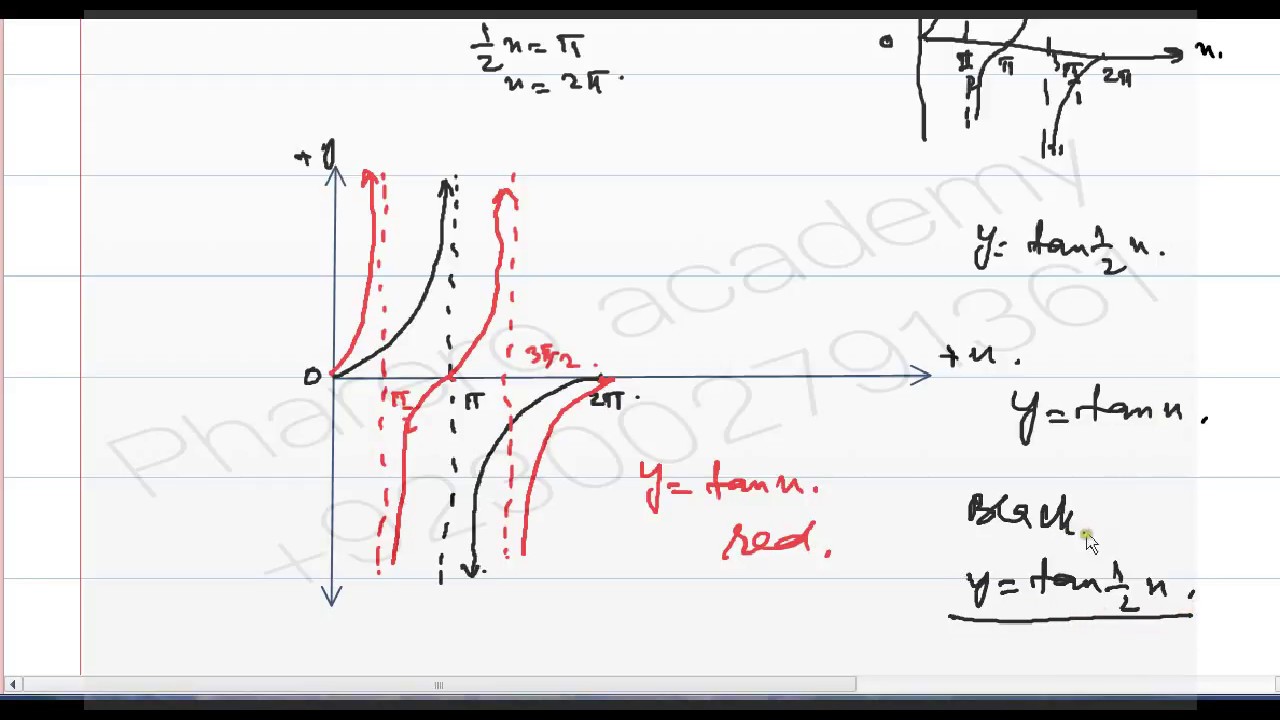


Graph Of Y Tan 1 2 X In Urdu Hindi Youtube



Solved Sketch The Graph Of The Function Include Two Ful Chegg Com



Graphing Tangent Ck 12 Foundation


Warm Upnov 25 Th Determine Whether To Us The Law Of Sine Or Cosine And Solve For The Missing Pieces 1 D Abc With A 12 B 13 C 24 2 D Abc Ppt Download
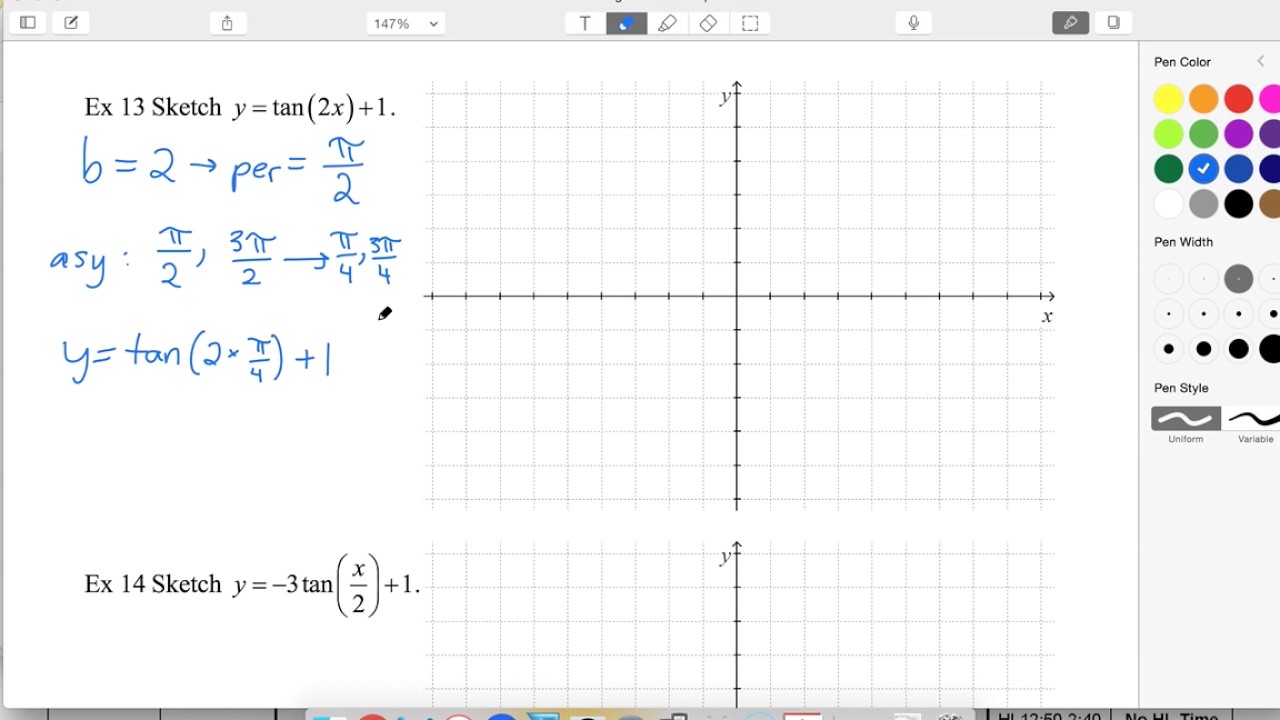


01 Ex13 Sketch Y Tan 2x 1 Youtube
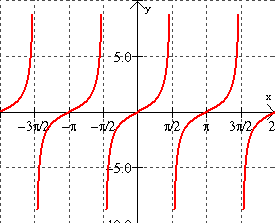


Tangent Cotangent Secant And Cosecant Graphs Mathbitsnotebook Ccss Math
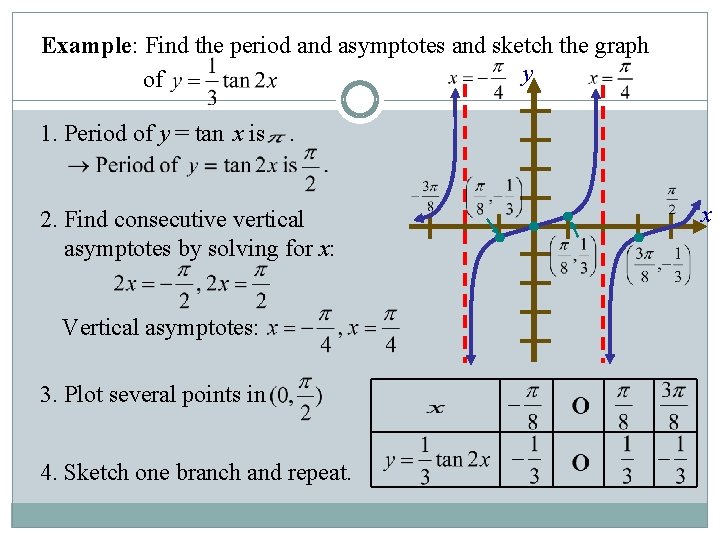


Unit 7 Trigonometric Functions Graphing The Trigonometric Function



Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Ppt Video Online Download


Trigonometry Functions User S Blog
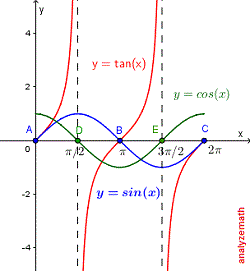


Graph Tangent And Cotangent


Bestmaths


Graph Tangent And Cotangent
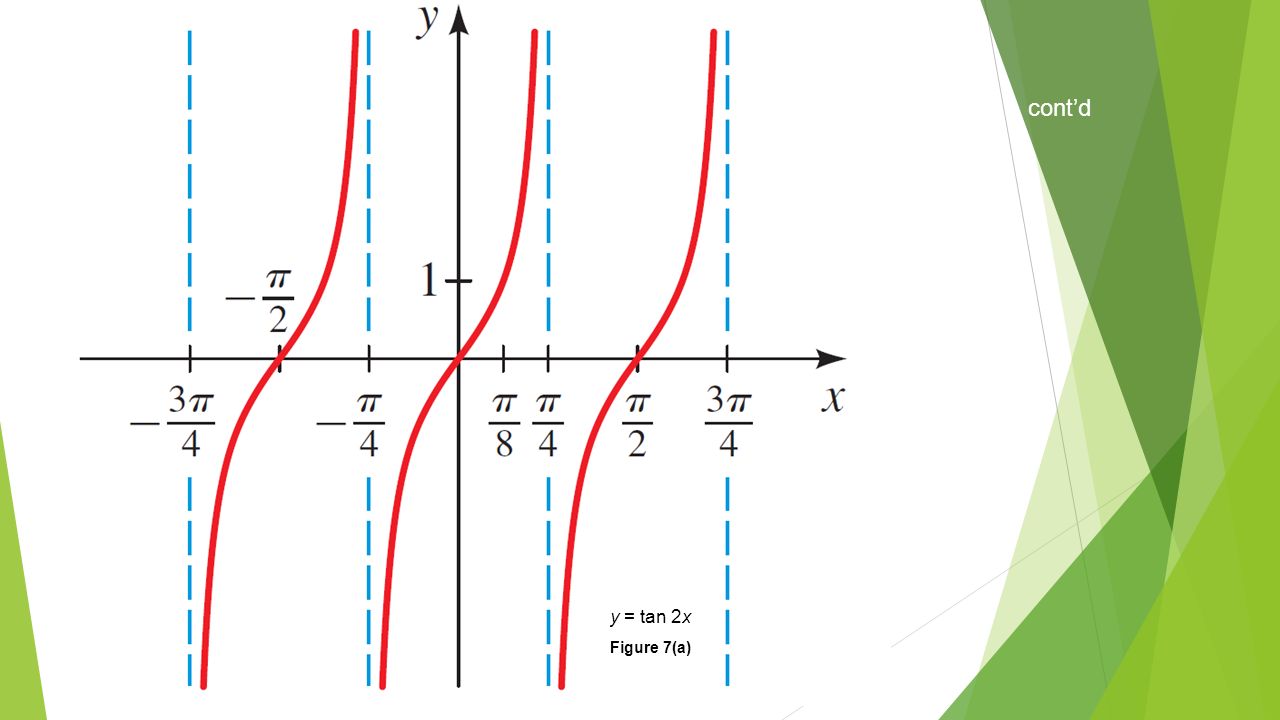


Graphs Of Tangent Cotangent Ppt Video Online Download
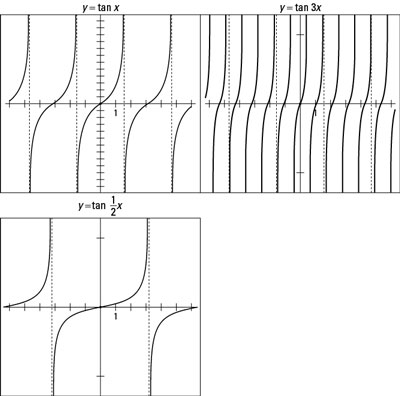


Graph Tangent Functions With Variable Multipliers Dummies
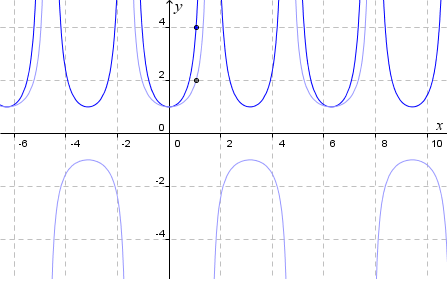


Explore The Slope Of The Tan Curve
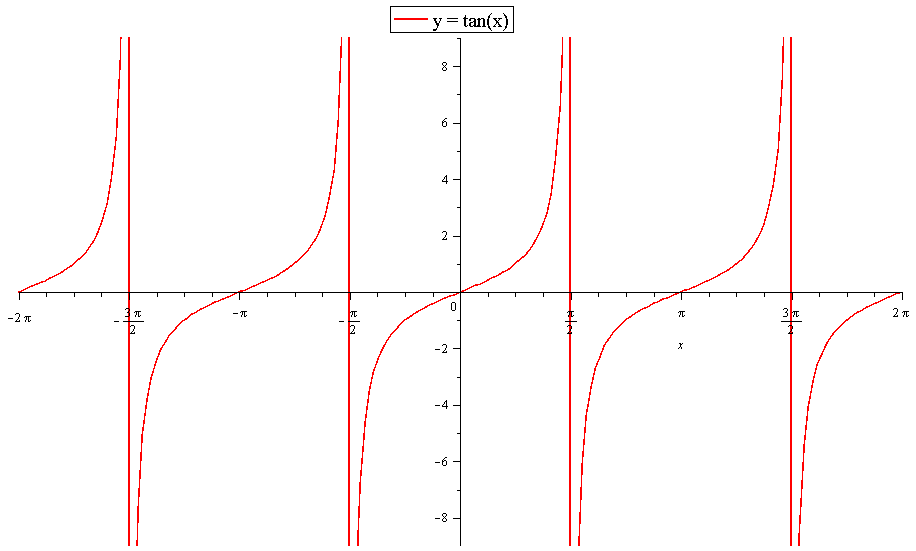


How Do You Graph Y Tan3x Socratic
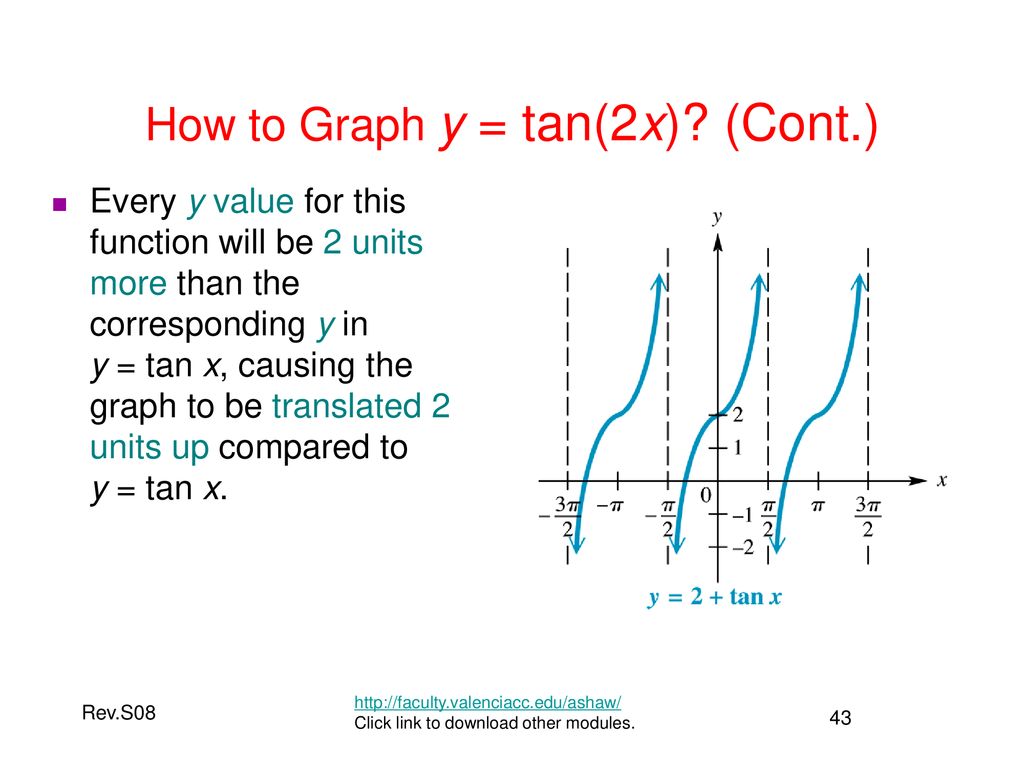


Graphs Of The Circular Functions Ppt Download
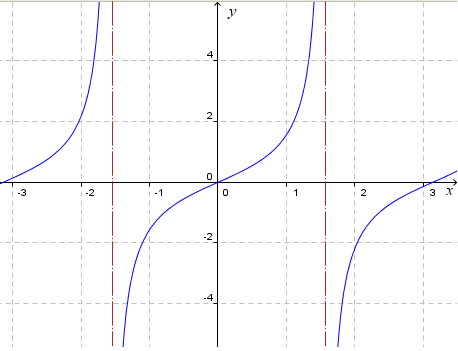


Explore The Slope Of The Tan Curve
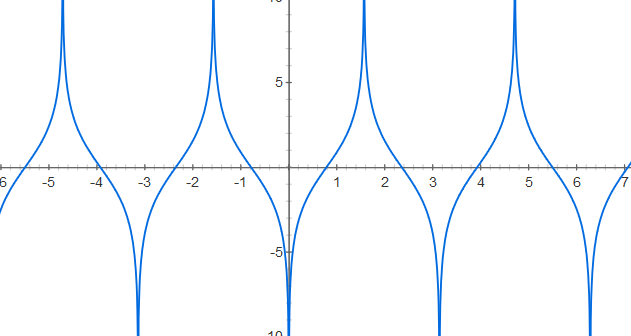


How Do You Graph Y Ln Tan 2 X Socratic
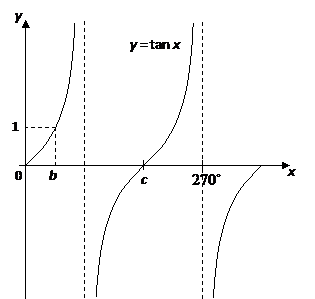


Tangent Graphs Worked Solutions Examples Videos


Biomath Trigonometric Functions



Graphing The Tangent Function Amplitude Period Phase Shift Vertical Shift Video Lesson Transcript Study Com
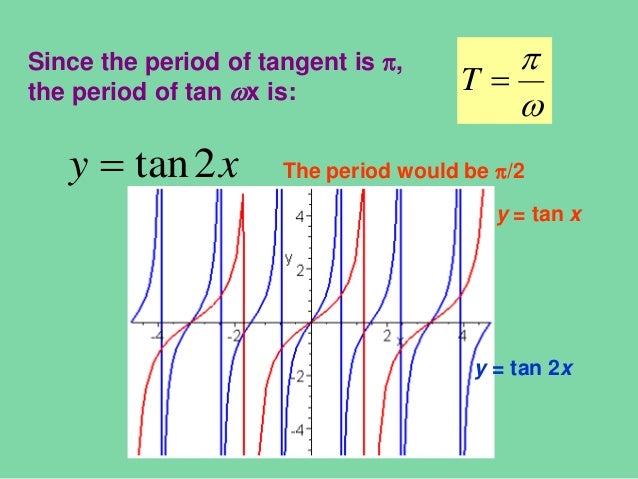


Graphs Of Other Trigonometric Functions Lecture


More Trigonometric Graphs Ppt Download


Graphs Of The Other Trigonometric Functions Algebra And Trigonometry
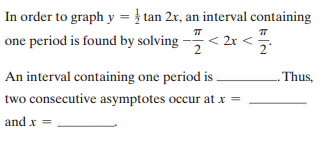


Answered In Order To Graph Y Tan 2x An Bartleby



0 件のコメント:
コメントを投稿